Углы Эйлера и анимация объектов

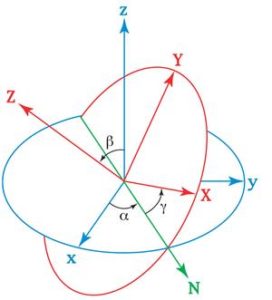
Углы Эйлера описывают поворот объекта в трёхмерном евклидовом пространстве. При этом рассматриваются две прямоугольные системы координат, имеющие общий центр: неподвижная система и подвижная, связанная с объектом. На рис.1 неподвижная система координат имеет обозначение XYZ (она наклонена), а подвижная система обозначена как xyz. Углы Эйлера представляют собой углы, на которые поворачивается подвижная система координат, связанная с объектом, до совмещения с неподвижной системой. В классическом варианте первый поворот происходит на угол α вокруг оси z, связанной с объектом, до тех пор, пока не произойдет совпадение оси x, связанной с объектом, c плоскостью XY неподвижной системы. Такое совпадение произойдет по линии пересечения плоскостей XY и xy (линия N на рис. 1). Следующий поворот осуществляется на угол β вокруг нового положения оси x, связанной с объектом, до тех пор, пока не совместятся оси аппликат обеих прямоугольных систем. При этом ось y, связанная с объектом, окажется в плоскости xy неподвижной системы координат XYZ. Последний поворот производится на угол γ вокруг нового положения оси аппликат подвижной системы координат (она будет совпадать с такой же осью неподвижной системы), после чего оси координат XY и xy совместятся.

Такие повороты некоммутативны, и конечное положение подвижной системы координат зависит от порядка, в котором совершаются повороты.

Если известны координаты вектора R(r_x, r_y, r_z) в подвижной системе координат XYZ и известны углы Эйлера (α, β, γ) подвижной системы координат xyz относительно неподвижной, то можно вычислить координаты этого вектора в неподвижной системе координат xyz. Для этого следует построить матрицы трех последовательных поворотов на углы α, β и γ:

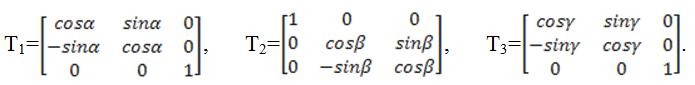
Перемножая эти матрицы в обратном порядке, получим итоговую ортогональную матрицу:

T=T₃×T₂×T₁,

которая преобразует координаты вектора R(r_x, r_y, r_z) подвижной системы координат в координаты вектора N(n_x, n_y, n_z) такой же длины в неподвижной системе координат:

N = T×R,

где N и R — матрицы-столбцы соответствующих координат.

Углы Эйлера являются наиболее естественными и понятными при выполнении различных операций вращения объектов, поскольку они соответствуют вращениям объекта, наблюдаемым в видовых окнах трехмерных графических систем. Однако их использование в системах компьютерной анимации сталкивается с рядом трудностей. Прежде всего, это необходимость выбора определенной последовательности поворотов объекта относительно осей системы координат. Если повернуть объект сначала вокруг оси X, затем вокруг оси Y и, наконец, вокруг оси Z, то это будет совсем не тот поворот, если бы повернуть этот объект на те же углы, но в другой последовательности.

Рассмотрим другой пример — создание анимации кубика при повороте его вокруг оси Z мировой системы координат на угол, превышающий 360°, например на угол 450°. Попробуем создать два ключевых кадра, между которыми кубик должен повернуться на этот угол. Для этого в программе MaxScript создайте стандартный параллелепипед:

b = box()

После этого переместите ползунок временной шкалы анимации к кадру 10, включите режим Auto Key, а затем выполните команду:

b.rotation.z_rotation = 450

Воспроизведите анимацию. Объект повернется только на 90°, поскольку его оборот на 360° будет игнорирован. Теперь то же самое проделайте в окне программы 3ds Max. Анимация объекта между двумя ключевыми кадрами произойдет на угол 450°. Таким образом, применение эйлеровых вращений в программах компьютерной графики, аналогичных MaxScript, ограничивается одновременным вращением на угол, не превышающий 360°. Однако это не мешает создавать анимацию вручную за экраном дисплея.

Другая проблема углов Эйлера заключается в наличии Gimbal lock, или шарнирного замка. Его появление зависит от выбора порядка поворотов объекта. Например, повернем объект вначале вокруг оси Z на угол 140°, затем вокруг оси X на угол 90°, а потом на угол 130° вокруг оси Y (рис. 2).

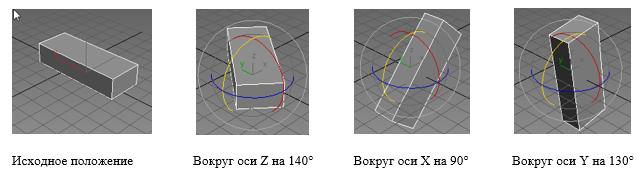
Если теперь заново выполнить ту же последовательность поворотов, например, на углы 10° вокруг оси Z, затем на 90° вокруг оси X, а потом на 0° вокруг оси Y, то получим тот же результат. Проблема заключается в том, что когда вращение вокруг оси X становится равным 90° или -90°, то локальная ось вращения Y становится параллельной оси Z, но с обратным направлением, и поэтому вращение вокруг нее вступает в конфликт с предыдущим вращением вокруг оси Z.

Шарнирный замок отсутствует у матриц и кватернионов. Кватернионы предоставляют удобное математическое обозначение положения и вращения объектов в пространстве. В сравнении с углами Эйлера, кватернионы позволяют проще комбинировать вращения, а также избежать проблемы, связанной с невозможностью поворота вокруг оси, независимо от совершённого вращения по другим осям. В сравнении с матрицами они обладают большей вычислительной устойчивостью и могут быть более эффективными. Кватернионы используют для выполнения вращений в компьютерной графике, робототехнике, игровых движках, навигации, молекулярной динамике и вообще везде, где возникают проблемы с углами Эйлера или матрицами.

Литература

1. Углы Эйлера и Gimbal lock [Электронный ресурс] / http://habrahabr.ru – Хабрахабр, 2006. – Режим доступа: http://habrahabr.ru/post/183116/. – Дата доступа: 10.10.2013.
2. Кватернионы и вращение пространства [Электронный ресурс] / http://ru.wikipedia.org/ – Википедия — свободная энциклопедия, 2001. – Режим доступа: http://ru.wikipedia.org/wiki/ Кватернионы_и_вращение_пространства. – Дата доступа: 11.10.2013.

Автор: Горелик А.Г.